| Combinaison entre un titre et une Obligation | ||
EM ( Rdt) = moyenne pondérée (par la proportion de l'actif dans le portefeuille) des rendements de chacun des deux actifs.
σ (Rdt Portefeuille) = Racine [ ( wa*σa)² + (wb*σb)² + 2*wa*wb*σaσb*ρ( Rdt A;Rdt B)
Où ρ , coefficient de corrélation = Cov ( Rdt A; Rdt B) / σaσb
| Risque et rendement d'un portefeuille composé de deux actifs | ||||||||
| Actif A | Actif B | |||||||
| Poids dans le protefeuille | 20% | 80% | ||||||
| Calcul de la covariance des rendements de A et de B | ||||||||
| Proba (Etat) | Rdt ( A) | Rdt (B) | Rdt (Port) | Pi*(Kia-Ema)*(Kib-Emb) | ||||
| 20% | Etat 1 | 30% | -20% | -10% | -0,015975 | |||
| 50% | Etat 2 | 15% | 18% | 17% | 0,0009375 | |||
| 30% | Etat 3 | -20% | 35% | 24% | -0,0160875 | |||
| EM( Rdt) | 8% | 16% | 14% | -0,031125 | Covariance | |||
| Ecart-type (Rendements) | 18,9% | 19,2% | ||||||
| Covariance ( Rdt A; Rdt B) | -0,031125 |  |
||||||
| Coeff de corrélation ( Rdt A; Rdt B) | -86% | |||||||
| Ecart-type Rdt du portefeuille | 12,3% | |||||||
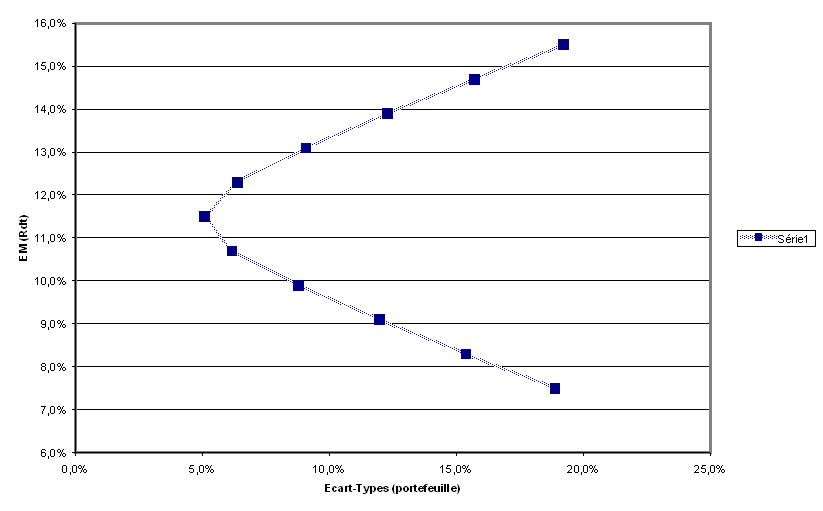
Objectif : Eliminer les mauvcais portefeuilles : mauvais voulant dire "ne répondant pas à la règle de Sharpe" , soit encore offrant un plus mauvais rendement pour un risque donné.
Dans l'exemple ci-dessus , compte tenu de l'anticorrélation des deux projets, le "ventre" apparaît visiblement, les portefeuilles supérieurs étant les "bons " portefeuilles. Ils se situent sur une frontière dite "efficiente".